-
KNN(K Neighbor Nearest)이란?IT 지식 창고 2019. 3. 25. 01:26
KNN ( K-Nearest Neighbor) In [1]:#주피터 노트북 블로그게시용 함수 from IPython.core.display import display, HTML display(HTML("<style> .container{width:100% !important;}</style>"))
KNN ( K -Nearest Neighbor) 개요¶
KNN은 K - 최근접 이웃법으로 분류 문제에 사용하는 알고리즘입니다.
새로운 데이터가 들어왔을 때 기존 데이터의 그룹 중 어떤 그룹에 속하는지 분류하는 문제를 말합니다.
실제 문제를 풀 때 자주 사용되지는 않지만, 이미지 분류 문제(딥러닝)에 대한 기본적인 접근방법입니다.
KNN의 하이퍼 파라미터는 탐색할 이웃 수(k), 거리 측정 방법 두가지 입니다.
k와, 거리 측정 방법에 따라 분류 경계면이 달라 진다는 이야기 입니다.
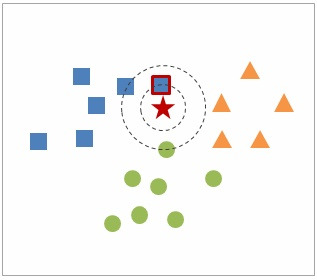
먼저 원리에 대해 간단히 그림으로 설명하자면,
KNN은 '새로 들어온 ★이 ■ 그룹의 데이터와 가장 가까우니 ★은 ■ 그룹이다.' 라고 분류하는 알고리즘입니다.
여기서 k의 역할은 몇 번째로 가까운 데이터까지 살펴볼 것인가를 정한 숫자입니다.
1) k에 따른 모형¶
k의 값이 너무 작으면, 데이터 하나하나에 영향을 받아 overfitting이 될 수 있고, k의 값이 너무 크면, 분류 경계면이 단조로워 underfitting이 될 수 있습니다.
이 때, 적합한 k를 결정하기 위해서는 cross - validation과 같은 방법을 이용하여, k를 보통 1~100사이의 값들로 그래프를 그려 Error가 제일 괜찮은 k를 선택합니다. 아래 그림처럼 k가 커지면 커질수록 Traing Errors는 한없이 감소하지만, Test Error는 감소하다가 다시 증가합니다.

2) 거리 척도 단위 문제¶
두 번째 하이퍼 파라미터로 거리를 정할수가 있습니다.
거리는 보통 유클리디안 거리(Euclidean Distance)를 자주 사용합니다. 그 외에도 수 많은 거리를 나타내는 척도가 많습니다. 궁금하면 https://ratsgo.github.io/machine%20learning/2017/04/17/KNN/ 이 분의 글을 보시면 될 것 같습니다.
일단 저는 유클리디안의 거리로 설명하겠습니다.
유클리디안의 거리는 아래의 식과 같습니다.
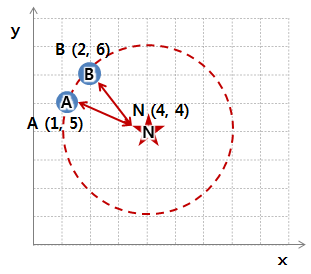
예를 들어, 아래의 그림에서 A-N 간의 유클리드 거리는 3.162 이고 B-N 간의 유클리드 거리는 2.828 로, B가 더 가깝다.
이때 A-N 간의 유클리드 거리는 3.162 이고 B-N 간의 유클리드 거리는 2.828 로, B가 더 가깝다.
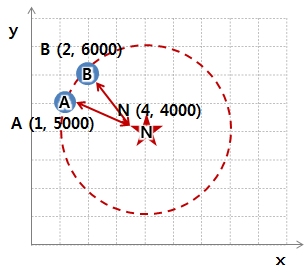
그런데 만약에 y좌표의 단위가 원(₩)으로 바뀌었다고 가정하자. 1달러 = 1,000원이라고 한다면 그래프가 아래처럼 바뀔 것입니다.
이때 A-N 간의 유클리드 거리는 1000.004 이고 B-N 간의 유클리드 거리는 2000.001 로, A가 더 가깝다.
이렇게 변수별 단위가 무엇이냐에 따라 거리가 달라지고, 가까운 순서도 달라집니다.
순서가 달라지면 KNN에서의 분류 결과도 달라진다는 뜻이다. 그래서 반드시 KNN 알고리즘을 적용할 때에는 데이터에 표준화를 해주어야 합니다.
3) KNN의 장단점¶
장점¶
특히 마할라노비스 거리와 같이 데이터의 분산을 고려할 경우 매우 강건(robust)한 방법론으로 알려져 있습니다.
알고리즘과 원리가 간단하여 구현하기가 쉽습니다.
수치 기반 데이터 분류 작업에서 성능이 좋다.
단점¶
그러나 최적 이웃의 수(k)와 어떤 거리척도가 분석에 적합한지 불분명해 데이터 각각의 특성에 맞게 연구자가 임의로 선정해야 하는 단점이 있습니다.
또 새로운 관측치와 각각의 학습 데이터 사이의 거리를 전부 측정해야 하므로 계산 시간이 오래 걸리는 한계점이 존재합니다.
차원(벡터)의 크기가 크면 계산량이 많아지고, 변수간 거리가 멀어지기 때문에 정확도가 떨어집니다.
이미지 참고 - https://kkokkilkon.tistory.com/14
KNN Algorithm - Titanic¶
In [2]:import numpy as np import pandas as pd import matplotlib.pyplot as plt
In [3]:#전처리가 다 되어있는 csv파일을 불러옵니다. train = pd.read_csv('titanic_train.csv') test = pd.read_csv('titanic_test.csv')
In [4]:train.head()
Out[4]:In [5]:test.head()
Out[5]:In [6]:#필요한 feature들만 남겨두고 열을 지웁니다. target = train['Survived'] train = train.drop(['PassengerId', 'Survived'], axis=1) passengerId = test['PassengerId'] test = test.drop(['PassengerId'], axis=1)
In [7]:#knn에서 표준화는 중요하기 때문에 표준화를 합니다. train = (train - train.mean())/train.std() test = (test - test.mean())/test.std()
In [8]:train.head()
Out[8]:In [9]:test.head()
Out[9]:In [10]:#KNN 알고리즘 함수 def KNearestNeighbor(train, target, test, k): size = len(test) class_result = [] for i in range(0,size) : # 유클리디안 거리 df = train - test.loc[i] #원래의 데이터와 판단하고자 하는 test데이터들 간의 차 df = df**2 #데이터의 제곱 train['Distance'] = np.sqrt(df.sum(axis=1))#데이터들의 합의 제곱근 = 거리 train['Survived'] = target train = train.sort_values(by='Distance', kind='mergesort') #거리 중 가까운 순서대로 정렬 train_head = train['Survived'].head(k) #정렬된 거리 중 본인이 선택한 k개만큼 추출 class_result.append(train_head.value_counts().index[0]) #그 중 가장 많은 결과를 도출 test['Survived'] = class_result return test
In [11]:#이제 KNN함수를 적용 시켜 봅니다. 저는 k=15로 지정하고 적용했습니다. test = KNearestNeighbor(train, target, test, 15) test.head(10)
Out[11]:In [12]:#다 만든 것을 Kaggle에 제출 해보았습니다. test['PassengerId'] = passengerId submission = test[['PassengerId' , 'Survived']]
In [13]:submission.to_csv('submission.csv', index=False)

알고리즘 참고 - https://cometouniverse.tistory.com/48
번외) K-Nearest Neighbor vs K-Means Clustering¶
간혹 K-Nearest Neighbor과 K-Means Clustering과 헷갈려 하시는 분들이 있습니다. 아마 K때문에 헷갈리는 것 같습니다.
이 두 방법은 사용하는 목적이 다릅니다.
K-Nearest Neighbor은 분류를 하기 위해 사용하는 알고리즘이고, K-Means는 주어진 데이터들이 어떤 특징들을 가지고 있는지 clustering이라고 하는 군집을 나누기 위해 사용하는 알고리즘입니다.
이 때 K-NN의 K는 분류 할때 k개의 데이터와 비교하여 분류할 때 사용하는 것이며 K-Means의 K는 k개의 군집으로 나누기 위해 사용하는 것입니다.
다시 말해, K-NN은 지도 학습(Surpervised Learning)이고, K-Means는 비지도 학습(Unsupervised Learing)입니다.
지도 학습은 예측(Prediction)하는 것이며, 위 Titanic에서 볼 수 있듯이 새로운 데이터에 대해서 어떠한 특징을 가진 사람들은 죽었고 또 다른 특징을 가진 사람들은 살았다라고 분류하는 것이다.
비지도 학습은 추론(inference)하는 것이며, 새로운 데이터가 아닌 기존에 주어져 있는 데이터들로만 죽은 사람들은 어떠한 특징을 가졌고 산 사람은 또 다른 특징을 가졌다라고 군집을 분석하는 것이다.
(주로 실생활에서는 암환자로 분류된 사람들은 여러 유전적으로 영향이 있다, 구매내역을 특징으로 한 구매자들의 그룹, 영화 시청자가 지정한 등급별로 그룹화된 영화 등.)
K-Means Clustering Algorithm¶

Step 1. 데이터를 k개의 그룹으로 random하게 할당한다. 위 그림에서 k는 3이다.
Iteration 1, Step 2a. 각 그룹의 중심(Centroid)를 구한다. (Centroid를 구하는 방법은 수학적이여서 여기서는 다루지 않겠습니다.)
Iteration 2, step 2b. 각 데이터들은 구한 3개의 Centroid중 가장 가까운 Centroid 그룹으로 다시 할당된다.
Iteration 2, Step 2a. 다시 각 그룹의 Centroid를 구한다.
Final Results. 더이상의 변화가 없을 때 까지 위 과정을 반복한다.
'IT 지식 창고' 카테고리의 다른 글
(Kaggle) 2019 2nd ML month KaKR - House Price (0) 2019.04.21 주가 예측 딥 러닝을 위한 자료들 (0) 2019.04.02 (Anaconda) anaconda를 통한 가상환경 생성/제거/연동 (0) 2019.03.19 (Kaggle) Titanic Machine Learning 입문 (0) 2019.01.31 split(), strip() (0) 2019.01.30 댓글